Thevenin's Theorem in AC Analysis

Source Transformation in AC Analysis

• Transform a voltage source in series with an impedance to a current source in     parallel with an impedance for simplification or vice versa.

Source transformations are easy to perform as long as there is a familiarity with Ohm's law. If there is a voltage source in series with an impedance, it is possible to find the value of the equivalent current source in parallel with the impedance by dividing the value of the voltage source by the value of the impedance. The converse also applies here: if a current source in parallel with an impedance is present, multiplying the value of the current source with the value of the impedance will result in the equivalent voltage source in series with the impedance.

Superposition Theorem in AC Analysis

The superposition theorem states that in a linear circuit with several sources, the current and voltage for any element in the circuit is the sum of the currents and voltages produced by each source acting independently. The theorem is valid for any linear circuit. The best way to use superposition with AC circuits is to calculate the complex effective or peak value of the contribution of each source applied one at a time, and then to add the complex values. This is much easier than using superposition with time functions, where one has to add the individual time functions.

To calculate the contribution of each source independently, all the other sources must be removed and replaced without affecting the final result.

When removing a voltage source, its voltage must be set to zero, which is equivalent to replacing the voltage source with a short circuit.

When removing a current source, its current must be set to zero, which is equivalent to replacing the current source with an open circuit. 

Now let's explore an example. 

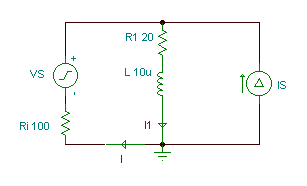
In the circuit shown below" 

R_i = 100 ohm, R₁ = 20 ohm, R₂ = 12 ohm, L = 10 uH, C = 0.3 nF, v_S(t)=50cos(wt) V, i_S(t)=1cos(wt+30°) A, f=400 kHz. 

Notice that both sources have the same frequency: we will only work in this chapter with sources all having the same frequency. Otherwise, superposition must be handled differently.

Find the currents i(t) and i₁(t) using the superposition theorem.

• REVIEW:
• The Superposition Theorem states that a circuit can be analyzed with only one source of power at a time, the corresponding component voltages and currents algebraically added to find out what they'll do with all power sources in effect.
• To negate all but one power source for analysis, replace any source of voltage (batteries) with a wire; replace any current source with an open (break).